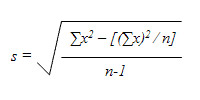Анализ данных: от простого к сложному
Есть мнение, что обработать данные, полученные в ходе количественного маркетингового исследования, не составляет особого труда. Однако не стоит недооценивать такой важный этап, как обработка данных. Такая работа требует специальных знаний таких дисциплин, как маркетинг, статистика, социология, программирование и др. Немаловажную роль играют практический опыт, навыки и осведомленность о событиях в микро- и макросреде.
Чтобы не загружать вас математикой приведу один выразительный и яркий пример, демонстрирующий необходимость взвешенного подхода к данным.
Пример: Одна крупная ИТ организация нашего города провела исследование двух своих филиалов и выяснила следующий факт:
«В двух отдельно стоящих офисах, открытых одновременно осенью 2002г., с одинаковым количеством работников, средний стаж работы сотрудников составил 7,5 лет в первом и 5,5 лет—во втором».
Исходные данные были обработаны и представлены как среднее арифметическое (табл. 1). В результате, ответственный специалист и директор компании сделали следующие выводы:
- Во втором офисе большая текучка
- Видимо, отсутствует мотивация сотрудников
- Зам. директора по персоналу должен быть уволен!
- Давайте дальше изучать причины увольнения сотрудников и т.д.
На первый взгляд, все правильно. Однако, на самом деле, выводы сделаны ложные и силы брошены на решение мнимой проблемы – ее просто нет!
Рассмотрение только одной средней величины при анализе маркетинговых и статистических данных может привести к ошибочным результатам.
Необходимо рассматривать ее в совокупности с такими величинами, характеризующими качество средней, как дисперсия (s2), среднеквадратичное отклонение (s) и стандартная ошибка средней (с. о.х).
Данные величины демонстрируют меру разброса изучаемых признаков. Для определения текучести кадров в рассмотренном примере нам понадобится один из перечисленных показателей – среднее квадратичное отклонение:
| Таблица 1. Среднее арифметическое | ||
| Исходные данные | ||
| №№ сотрудника | Стаж работы у сотрудников, в количестве лет | |
| Первый офис | Второй офис | |
| 1 | 21 | 1 |
| 2 | 1 | 5 |
| 3 | 1 | 1 |
| 4 | 9 | 10 |
| 5 | 4 | 1 |
| 6 | 3 | 22 |
| 7 | 19 | 5 |
| 8 | 4 | 6 |
| 9 | 10 | 20 |
| 10 | 7 | 3 |
| 11 | 2 | 4 |
| 12 | 6 | 2 |
| 13 | 6 | 9 |
| 14 | 7 | 1 |
| 15 | 4 | 21 |
| 16 | 6 | 4 |
| 17 | 22 | 4 |
| 18 | 3 | 22 |
| 19 | 21 | 1 |
| 20 | 1 | 3 |
| 21 | 1 | 2 |
| 22 | 9 | 1 |
| 23 | 4 | 4 |
| 24 | 3 | 1 |
| 25 | 7 | 2 |
| 26 | 2 | 2 |
| 27 | 10 | 3 |
| 28 | 22 | 3 |
| 29 | 1 | 1 |
| 30 | 9 | 1 |
| Среднее арифметическое | 7,5 | 5,5 |
Ниже демонстрируется таблица статистических данных по двум предприятиям с показателями средней арифметической величины и среднего квадратичного отклонения.
| Таблица 2. Среднее арифметическое и среднее квадратическое по двум офисам | ||
|
| Первый офис | Второй офис |
| Среднее арифметическое | 7,5 | 5,5 |
| Среднее квадратичное отклонение | 6,64 | 6,57 |
В данном случае среднее квадратичное отклонение может использоваться для сравнения текучести кадров на разных предприятиях. Как мы видим, у обоих предприятий средний срок пребывания сотрудника в должности составляет 6,6 лет, т. е. текучесть кадров в двух офисах практически одинаковая.
Таким образом, прежнее утверждение, основанное на средней арифметической, является ложным.
РЕЗЮМЕ: Этот небольшой пример очень выразительно демонстрирует необходимость качественной и компетентной аналитики данных. Доверяйте анализ данных только настоящим специалистам!
Иванов Павел Вячеславович, директор ООО "Маркетинговый центр "Максима"